Задача 1 . Один из углов параллелограмма равен 65°. Найти остальные углы параллелограмма.

∠C =∠A = 65° как противоположные углы параллелограмма.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма.

∠В = 180° — ∠А = 180° — 65° = 115°.

∠D =∠B = 115° как противолежащие углы параллелограмма.

Ответ: ∠А =∠С = 65°; ∠В =∠D = 115°.

Задача 2. Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.

Так как у параллелограмма имеется 2 равных острых угла и 2 равных тупых угла, то нам дана сумма двух тупых углов, т.е. ∠В +∠D = 220°. Тогда ∠В =∠D = 220°: 2 = 110°.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма, поэтому ∠А = 180° — ∠В = 180° — 110° = 70°. Тогда ∠C =∠A = 70°.

Ответ: ∠А =∠С = 70°; ∠В =∠D = 110°.

Задача 3. Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.

Пусть ∠А =х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение.

х = 180 : 4;

Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.

Противолежащие углы параллелограмма равны, следовательно,

∠А =∠С = 45°; ∠В =∠D = 135°.

Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.

Задача 4. Докажите, что если у четырехугольника две стороны параллельны и равны, то этот четырехугольник – параллелограмм.

Доказательство.

Проведем диагональ BD и рассмотрим Δ ADB и Δ CBD.

AD = BC по условию. Сторона BD – общая. ∠1 = ∠2 как внутренние накрест лежащие при параллельных (по условию) прямых AD и BC и секущей BD. Следовательно, Δ ADB = Δ CBD по двум сторонам и углу между ними (1-й признак равенства треугольников). В равных треугольниках соответственные углы равны, значит, ∠3 =∠4. А эти углы являются внутренними накрест лежащими при прямых AB и CD и секущей BD. Отсюда следует параллельность прямых AB и CD. Таким образом, в данном четырехугольнике ABCD противолежащие стороны попарно параллельны, следовательно, по определению ABCD – параллелограмм, что и требовалось доказать.

Задача 5. Две стороны параллелограмма относятся как 2 : 5, а периметр равен 3,5 м. Найти стороны параллелограмма.

∙ (AB + AD).

Обозначим одну часть через х. тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:

2 ∙ (2x + 5x) = 3,5;

2 ∙ 7x = 3,5;

x = 3,5 : 14;

Одна часть составляет 0,25 м. Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.

Проверка.

Периметр параллелограмма P ABCD = 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (м).

Так как противоположные стороны параллелограмма равны, то CD = AB = 0,25 м; BC = AD = 1,25 м.

Ответ: CD = AB = 0,25 м; BC = AD = 1,25 м.

Параллелограммом называют четырехугольник противолежащие стороны которого попарно параллельны. Также параллелограмм владеет такими свойствами, как противоположные стороны равны, противоположные углы равны, сумма всех углов равна 360 градусов.

Вам понадобится

• Знания по геометрии.

Инструкция

1. Представим дан один из углов параллелограмма и равен A. Обнаружим значения остальных 3. По свойству параллелограмма противоположные углы равны. Значит угол, лежащий наоборот данного равен данному и его значение равно А.

2. Обнаружим оставшиеся два угла. Потому что сумма всех углов в параллелограмме равна 360 градусов, а противоположные углы между собой равны, то получается, что угол, принадлежащий одной стороне с данным, равен (360 — 2А)/2. Ну либо позже реформирования получим 180 — А. Таким образом в параллелограмме два угла равны А, а два других угла равны 180 — А.

Обратите внимание!
Значение одного угла не может превышать 180 градусов. Полученные значения углов дозволено легко проверить. Для этого сложите их и, если сумма равна 360, все посчитано правильно.

Полезный совет
Прямоугольник и ромб являются частным случаем параллелограмма, следственно все свойства и способы вычисления углов применимы и к ним.

Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т.е. лежат на параллельных прямых

Свойства параллелограмма: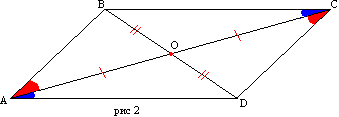
Теорема 22. Противоположные стороны параллелограма равны.
Доказательство. В параллелограмме АВСD проведем диагональ АС. Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠ САВ=∠ АСD, ∠ АСВ=∠ DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч.т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников:
Теорема 23. Противоположные углы параллелограмма равны: ∠ А=∠ С и ∠ В=∠ D.
Равенство первой пары идет из равенства треугольников АВD и CBD, а второй - АВС и ACD.
Теорема 24. Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов.
Это так, потому что они являются внутренними односторонними углами.
Теорема 25. Диагонали параллелограмма делят друг друга в точке их пересечения пополам.
Доказательство. Рассмотрим треугольники ВОС и АОD. По первому свойству AD=ВС ∠ ОАD=∠ ОСВ и ∠ ОDА=∠ ОВС как накрест лежащие при параллельных прямых AD и ВС. Поэтому треугольники ВОС и АОD равны по стороне и прилежащим к ней углам. Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д.

Признаки параллелограмма
Теорема 26. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом.
Доказательство. Пусть у четырехугольника АВСD стороны AD и ВС, АВ и CD соответственно равны (рис2). Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.
Теорема 27. Если противоположные углы четырехугольника попарно равны, то он является параллелограммом.
Пусть ∠ А=∠ С и ∠ В=∠ D. Т.к. ∠ А+∠ В+∠ С+∠ D=360 о, то ∠ А+∠ В=180 о и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению.
Теорема 28. Если соседние углы четырехугольника, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов, то он является параллелограммом.
Если внутренние односторонные углы в сумме составляют 180 градусов, то прямые праллельны. Значит АВ парал CD и ВС парал AD. Четырехугольник оказывается параллелограммом по определению.
Теорема 29. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник - параллелограмм.
Доказательство. Если АО=ОС, ВО=ОD, то треугольники АOD и ВОС равны, как имеющие равны углы (вертикальные) при вершине О, заключенные между парами равных сторон. Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по признаку 1.
Теорема 30. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом.
Пусть в четырехугольнике АВСD стороны АВ и CD параллельны и равны. Проведем диагонали АС и ВD. Из параллельности этих прямых следует равенство накрест лежащих углов АВО=СDО и ВАО=ОСD. Треугольники АВО и CDО равны по стороне и прилежащим к ней углам. Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом по признаку 4.

В геометрии рассматривают частные случаи параллелограмма.

Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны, т. е. лежат на параллельных прямых (рис.1).

Теорема 1. О свойстве сторон и углов параллелограмма. В параллелограмме противоположные стороны равны, противоположные углы равны и сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.

Доказательство. В данном параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC (рис.2).

Эти треугольники равны, так как ∠ 1 = ∠ 4, ∠ 2 = ∠ 3 (накрест лежащие углы при параллельных прямых), а сторона АС общая. Из равенства Δ ABC = Δ ADC следует, что АВ = CD, ВС = AD, ∠ B = ∠ D. Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых. Теорема доказана.

Замечание. Равенство противоположных сторон параллелограмма означает, что отрезки параллельных, отсекаемых параллельными, равны.

Следствие 1. Если две прямые параллельны, то все точки одной прямой находятся на одном и том же расстоянии от другой прямой.

Доказательство. В самом деле, пусть а || b (рис.3).

Проведем из каких-нибудь двух точек В и С прямой b перпендикуляры ВА и CD к прямой а. Так как АВ || CD, то фигура ABCD - параллелограмм, и следовательно, АВ = CD.

Расстоянием между двумя параллельными прямыми называется расстояние от произвольной точки одной из прямых до другой прямой.

По доказанному оно равно длине перпендикуляра, проведенного из какой-нибудь точки одной из параллельных прямых к другой прямой.

Пример 1. Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найти стороны параллелограмма.

Решение. По теореме 1 противоположные стороны параллелограмма равны. Обозначим одну сторону параллелограмма через х, другую через у. Тогда по условию $$\left\{\begin{matrix} 2x + 2y = 122 \\x - y = 25 \end{matrix}\right.$$ Решая эту систему, получим х = 43, у = 18. Таким образом, стороны параллелограмма равны 18, 43, 18 и 43 см.

Пример 2.

Решение. Пусть условию задачи отвечает рисунок 4.

Обозначим АВ через х, а ВС через у. По условию периметр параллелограмма равен 10 см, т. е. 2(x + у) = 10, или х + у = 5. Периметр треугольника ABD равен 8 см. А так как АВ + AD = х + у = 5 то BD = 8 - 5 = 3 . Итак, BD = 3 см.

Пример 3. Найти углы параллелограмма, зная, что один из них больше другого на 50°.

Решение. Пусть условию задачи отвечает рисунок 5.

Обозначим градусную меру угла А через х. Тогда градусная мера угла D равна х + 50°.

Углы BAD и ADC внутренние односторонние при параллельных прямых АВ и DC и секущей AD. Тогда сумма этих названных углов составит 180°, т. е.
х + х + 50° = 180°, или х = 65°. Таким образом, ∠ A = ∠ C = 65°, a ∠ B = ∠ D = 115°.

Пример 4. Стороны параллелограмма равны 4,5 дм и 1,2 дм. Из вершины острого угла проведена биссектриса. На какие части делит она большую сторону параллелограмма?

Решение. Пусть условию задачи отвечает рисунок 6.

АЕ - биссектриса острого угла параллелограмма. Следовательно, ∠ 1 = ∠ 2.

Средний уровень

Параллелограмм, прямоугольник, ромб, квадрат (2019)

1. Параллелограмм

Сложное слово «параллелограмм »? А скрывается за ним очень простая фигура.

Ну, то есть, взяли две параллельные прямые:

Пересекли ещё двумя:

И вот внутри - параллелограмм !

Какие же есть свойства у параллелограмма?

Свойства параллелограмма.

То есть, чем можно пользоваться, если в задаче дан параллелограмм ?

На этот вопрос отвечает следующая теорема:

Давай нарисуем все подробно.

Что означает первый пункт теоремы ? А то, что если у тебя ЕСТЬ параллелограмм, то непременно

Второй пункт означает, что если ЕСТЬ параллелограмм , то, опять же, непременно :

Ну, и наконец, третий пункт означает, что если у тебя ЕСТЬ параллелограмм, то обязательно:

Видишь, какое богатство выбора? Что же использовать в задаче? Попробуй ориентироваться на вопрос задачи, или просто пробуй все по очереди - какой-нибудь «ключик» да подойдёт.

А теперь зададимся другим вопросом: а как узнать параллелограмм «в лицо»? Что такое должно случиться с четырехугольником, чтобы мы имели право выдать ему «звание» параллелограмма?

На этот вопрос отвечает несколько признаков параллелограмма.

Признаки параллелограмма.

Внимание! Начинаем.

Паралелограмм.

Обрати внимание : если ты нашёл хотя бы один признак в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмма.

2. Прямоугольник

Думаю, что для тебя вовсе не явится новостью то, что

Первый вопрос: а является ли прямоугольник параллелограммом?

Конечно, является! Ведь у него и - помнишь, наш признак 3 ?

А отсюда, конечно же, следует, что у прямоугольника, как и у всякого параллелограмма и, а диагонали точкой пересечения делятся пополам.

Но есть у прямоугольника и одно отличительное свойство.

Свойство прямоугольника

Почему это свойство отличительное? Потому что ни у какого другого параллелограмма не бывает равных диагоналей. Сформулируем более чётко.

Обрати внимание : чтобы стать прямоугольником, четырехугольнику нужно сперва стать параллелограммом, а потом уже предъявлять равенство диагоналей.

3. Ромб

И снова вопрос: ромб - это параллелограмм или нет?

С полным правом - параллелограмм , потому что у него и (вспоминаем наш признак 2 ).

И снова, раз ромб - параллелограмм , то он обязан обладать всеми свойствами параллелограмма. Это означает, что у ромба противоположные углы равны, противоположные стороны параллельны, а диагонали делятся точкой пересечения пополам.

Свойства ромба

Посмотри на картинку:

Как и в случае с прямоугольником, свойства эти - отличительные , то есть по каждому из этих свойств можно заключить, что перед нами не просто параллелограмм , а именно ромб.

Признаки ромба

И снова обрати внимание : должен быть не просто четырехугольник, у которого перпендикулярны диагонали, а именно параллелограмм . Убедись:

Нет, конечно, хотя его диагонали и перпендикулярны, а диагональ - биссектриса углов и. Но … диагонали не делятся, точкой пересечения пополам, поэтому - НЕ параллелограмм , а значит, и НЕ ромб .

То есть квадрат - это прямоугольник и ромб одновременно. Давай посмотрим, что из этого получится.

Понятно почему? - ромб - биссектриса угла A, который равен. Значит делит (да и тоже) на два угла по.

Ну, это совсем ясно: прямоугольник диагонали равны; ромб диагонали перпендикулярны, и вообще - параллелограмм диагонали делятся точкой пересечения пополам.

СРЕДНИЙ УРОВЕНЬ

Свойства четырехугольников. Параллелограмм

Свойства параллелограмма

Внимание! Слова «свойства параллелограмма » означают, что если у тебя в задаче есть параллелограмм, то всем нижеследующим можно пользоваться.

Теорема о свойствах параллелограмма.

В любом параллелограмме:

Давай-ка поймём, почему это всё верно, иными словами ДОКАЖЕМ теорему.

Итак, почему верно 1)?

Раз - параллелограмм, то:

• как накрест лежащие
• как накрест лежащие.

Значит, (по II признаку: и - общая.)

Ну вот, а раз, то и - всё! - доказали.

Но кстати! Мы ещё доказали при этом и 2)!

Почему? Но ведь (смотри на картинку), то есть, а именно потому, что.

Осталось только 3).

Для этого всё-таки придётся провести вторую диагональ.

И теперь видим, что - по II признаку (угла и сторона «между» ними).

Свойства доказали! Перейдём к признакам.

Признаки параллелограмма

Напомним, что признак параллелограмма отвечает на вопрос "как узнать?", что фигура является параллелограммом.

В значках это так:

Почему? Хорошо бы понять, почему - этого хватит. Но смотри:

Ну вот и разобрались, почему признак 1 верен.

Ну, это ещё легче! Снова проведём диагональ.

А значит:

И тоже несложно. Но …по-другому!

Значит, . Ух! Но и - внутренние односторонние при секущей!

Поэтому тот факт, что означает, что.

А если посмотришь с другой стороны, то и - внутренние односторонние при секущей! И поэтому.

Видишь, как здорово?!

И опять просто:

Точно так же, и.

Обрати внимание: если ты нашел хотя бы один признак параллелограмма в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмма.

Для полной ясности посмотри на схему:

Свойства четырехугольников. Прямоугольник.

Свойства прямоугольника:

Пункт 1) совсем очевидный - ведь просто выполнен признак 3 ()

А пункт 2) - очень важный . Итак, докажем, что

А значит, по двум катетам (и - общий).

Ну вот, раз треугольники и равны, то у них и гипотенузы и тоже равны.

Доказали, что!

И представь себе, равенство диагоналей - отличительное свойство именно прямоугольника среди всех параллелограммов. То есть верно такое утверждение^

Давай поймём, почему?

Значит, (имеются в виду углы параллелограмма). Но ещё раз вспомним, что - параллелограмм, и поэтому.

Значит, . Ну и, конечно, из этого следует, что каждый из них по! Ведь в сумме-то они должны давать!

Вот и доказали, что если у параллелограмма вдруг (!) окажутся равные диагонали, то это точно прямоугольник .

Но! Обрати внимание! Речь идёт о параллелограммах ! Не любой четырехугольник с равными диагоналями - прямоугольник, а только параллелограмм!

Свойства четырехугольников. Ромб

И снова вопрос: ромб - это параллелограмм или нет?

С полным правом - параллелограмм, потому что у него и (Вспоминаем наш признак 2).

И снова, раз ромб - параллелограмм, то он обязан обладать всеми свойствами параллелограмма. Это означает, что у ромба противоположные углы равны, противоположные стороны параллельны, а диагонали делятся точкой пересечения пополам.

Но есть и особенные свойства. Формулируем.

Свойства ромба

Почему? Ну, раз ромб - это параллелограмм, то его диагонали делятся пополам.

Почему? Да, потому же!

Иными словами, диагонали и оказались биссектрисами углов ромба.

Как в случае с прямоугольником, свойства эти - отличительные , каждые из них является ещё и признаком ромба.

Признаки ромба.

А это почему? А посмотри,

Значит, и оба этих треугольника - равнобедренные.

Чтобы быть ромбом, четырёхугольник сперва должен «стать» параллелограммом, а потом уже демонстрировать признак 1 или признак 2.

Свойства четырехугольников. Квадрат

То есть квадрат - это прямоугольник и ромб одновременно. Давай посмотрим, что из этого получится.

Понятно, почему? Квадрат - ромб - биссектриса угла, который равен. Значит делит (да и тоже) на два угла по.

Ну, это совсем ясно: прямоугольник диагонали равны; ромб диагонали перпендикулярны, и вообще - параллелограмм диагонали делятся точкой пересечения пополам.

Почему? Ну, просто применим теорему Пифагора к.

КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ

Свойства параллелограмма:

1. Противоположные стороны равны: , .
2. Противоположные углы равны: , .
3. Углы при одной стороне составляют в сумме: , .
4. Диагонали делятся точкой пересечения пополам: .

Свойства прямоугольника:

1. Диагонали прямоугольника равны: .
2. Прямоугольник - параллелограмм (для прямоугольника выполняются все свойства параллелограмма).

Свойства ромба:

1. Диагонали ромба перпендикулярны: .
2. Диагонали ромба являются биссектрисами его углов: ; ; ; .
3. Ромб - параллелограмм (для ромба выполняются все свойства параллелограмма).

Свойства квадрата:

Квадрат - ромб и прямоугольник одновременно, следовательно для квадрата выполняются все свойства прямоугольника и ромба. А так же.