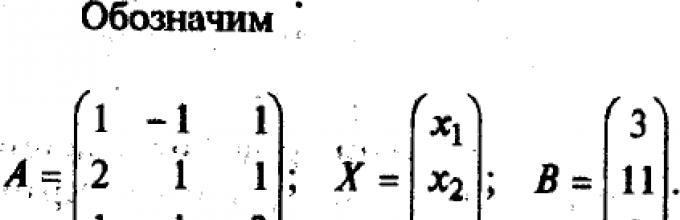Система уравнений метод сложения. Методы решения систем уравнений

Системой линейных уравнений с двумя неизвестными - это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:

{ a1*x + b1*y = c1,
{ a2*x + b2*y = c2

Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 - некоторые вещественные числа. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения.

Алгоритм решения способом сложения

Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.

1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.

2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным

3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.

4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.

5. Сделать проверку решения.

Пример решения способом сложения

Для большей наглядности решим способом сложения следующую систему линейных уравнений с двумя неизвестными:

{3*x + 2*y = 10;
{5*x + 3*y = 12;

Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у. Для этого умножим первое уравнение на три, а второе уравнение на два.

{3*x+2*y=10 |*3
{5*x + 3*y = 12 |*2

Получим следующую систему уравнений:

{9*x+6*y = 30;
{10*x+6*y=24;

Теперь из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.

10*x+6*y - (9*x+6*y) = 24-30; x=-6;

Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.

{3*(-6) + 2*y =10;
{2*y=28; y =14;

Получилась пара чисел x=6 и y=14. Проводим проверку. Делаем подстановку.

{3*x + 2*y = 10;
{5*x + 3*y = 12;

{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;

{10 = 10;
{12=12;

Как видите, получились два верных равенства, следовательно, мы нашли верное решение.

Рассмотрим вначале случай, когда число уравнений равно числу переменных, т.е. m = n. Тогда матрица системы - квадратная, а ее определитель называют определителем системы.

Метод обратной матрицы

Рассмотрим в общем виде систему уравнений АХ = В с невырожденной квадратной матрицей А. В этом случае существует обратная матрица А -1 . Домножим слева обе части на А -1 . Получим А -1 АХ = А -1 В. Отсюда ЕХ = А -1 В и

Последнее равенство представляет собой матричную формулу для нахождения решения таких систем уравнений. Использование этой формулы получило название метода обратной матрицы

Например, решим этим методом следующую систему:

;

В конце решения системы можно сделать проверку, подставив найденные значения в уравнения системы. При этом они должны обратиться в верные равенства.

Для рассмотренного примера проведем проверку:

Метод решения систем линейных уравнений с квадратной матрицей по формулам Крамера

Пусть n= 2:

Если обе части первого уравнения умножить на a 22 , а обе части второго – на (-a 12), и затем сложить полученные уравнения, то мы исключим из системы переменнуюx 2 . Аналогично можно исключить переменнуюx 1 (умножив обе части первого уравнения на (-a 21), а обе части второго – наa 11). В результате получим систему:

Выражение в скобках есть определитель системы

Обозначим

Тогда система примет вид:

Из полученной системы следует, что если определитель системы 0, то система будет совместной и определенной. Ее единственное решение можно вычислить по формулам:

Если = 0, а 1 0 и/или 2 0, то уравнения системы примут вид 0*х 1 = 2 и/или0*х 1 = 2 . В этом случае система будет несовместной.

В случае, когда = 1 = 2 = 0, система будет совместной и неопределенной (будет иметь бесконечное множество решений), так как примет вид:

Теорема Крамера (доказательство опустим). Если определитель матрицы системыnуравненийне равен нулю, то система имеет единственное решение, определяемое по формулам:

где  j - определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов.

Вышеприведенные формулы называют формулами Крамера .

В качестве примера решим этим методом систему, которую до этого решали методом обратной матрицы:

Недостатки рассмотренных методов:

1) существенная трудоемкость (вычисление определителей и нахождение обратной матрицы);

2) ограниченная область применения (для систем с квадратной матрицей).

Реальных экономические ситуации чаще моделируются системами, в которых число уравнений и переменных довольно значительное, причем уравнений больше, чем переменных Поэтому на практике более распространен следующий метод.

Метод Гаусса (метод последовательного исключения переменных)

Этот метод используется для решения системы m линейных уравнений с n переменными в общем виде. Его суть заключается в применении к расширенной матрице системы равносильных преобразований, с помощью которых система уравнений преобразуется к виду, когда ее решения становится легко найти (если они есть).

Это такой вид, в котором левая верхняя часть матрицы системы будет представлять собой ступенчатую матрицу. Этого добиваются с помощью тех же приемов, с помощью которых получали ступенчатую матрицу с целью определения ранга. При этом применяют к расширенной матрице элементарные преобразования, которые позволят получить равносильную систему уравнений. После этого расширенная матрица примет вид:

Получение такой матрицы называют прямым ходом метода Гаусса.

Нахождение из соответствующей системы уравнений значений переменных называют обратным ходом метода Гаусса. Рассмотрим его.

Отметим, что последние (m – r) уравнений примут вид:

Если хотя бы одно из чисел
не равно нулю, то соответствующее равенство будет ложным, а вся система несовместной.

Поэтому для любой совместной системы
. В этом случае последние (m – r) уравнений при любых значениях переменных будут тождествами 0 = 0, и их можно не принимать во внимание при решении системы (просто отбросить соответствующие строки).

После этого система примет вид:

Рассмотрим вначале случай, когда r=n. Тогда система примет вид:

Из последнего уравнения системы можно однозначно найти x r .

Зная x r , из него можно однозначно выразитьx r -1 . Затем из предыдущего уравнения, знаяx r иx r -1 , можно выразитьx r -2 и т.д. доx 1 .

Итак, в этом случае система будет совместной и определенной.

Теперь рассмотрим случай, когда rбазисными (основными), а все остальные –небазисными (неосновными, свободными). Последнее уравнение системы будет иметь вид:

Из этого уравнения можно выразить базисную переменную x r через небазисные:

Предпоследнее уравнение будет иметь вид:

Подставив в него вместо x r полученное выражение, можно будет выразить базисную переменнуюx r -1 через небазисные. И т.д. до переменнойx 1 . Чтобы получить решение системы, можно приравнять небазисные переменные к произвольным значениям и после этого вычислить базисные переменные по полученным формулам. Таким образом, в этом случае система будет совместной и неопределенной (иметь бесконечное множество решений).

Например, решим систему уравнений:

Совокупность базисных переменных будем называть базисом системы. Совокупность столбцов коэффициентов при них тоже будем называтьбазисом (базисными столбцами), илибазисным минором матрицы системы. То решение системы, в котором все небазисные переменные равны нулю, будем называтьбазисным решением .

В предыдущем примере базисным решением будет (4/5; -17/5; 0; 0) (переменные х 3 и х 4 (с 1 и с 2) приравнены к нулю, а базисные переменные х 1 и х 2 рассчитаны через них). Чтобы привести пример небазисного решения, надо приравнять х 3 и х 4 (с 1 и с 2) к произвольным числам, неравным одновременно нулю, и рассчитать через них остальные переменные. Например, при с 1 = 1 и с 2 = 0 получим небазисное решение – (4/5; -12/5; 1; 0). Подстановкой легко убедиться, что оба решения – верные.

Очевидно, что в неопределенной системе небазисных решений может быть бесконечно много. Сколько может быть базисных решений? Каждой строке преобразованной матрицы должна соответствовать одна базисная переменная. Всего в задаче nпеременных, а базисных строк –r. Поэтому число всевозможных наборов базисных переменных не может превысить число сочетаний изnпоr 2 . Оно может быть меньше, чем , потому что не всегда можно преобразовать систему к такому виду, чтобы именно этот набор переменных был базисным.

Что это за вид? Это такой вид, когда матрица, образованная из столбцов коэффициентов при этих переменных, будет ступенчатой, и при этом будет состоять из rстрок. Т.е. ранг матрицы коэффициентов при этих переменных должен быть равенr. Большеrон быть не может, так как число столбцов равноr. Если он окажется меньшеr, то это говорит о линейной зависимости столбцов при переменных. Такие столбцы не могут составить базис.

Рассмотрим, какие еще базисные решения могут быть найдены в рассмотренном выше примере. Для этого рассмотрим всевозможные сочетания из четырех переменных по две базисных. Таких сочетаний будет
, причем одно из них (х 1 и х 2) уже было рассмотрено.

Возьмем переменные х 1 и х 3 . Найдем ранг матрицы коэффициентов при них:

Так как он равен двум, они могут быть базисными. Приравняем небазисные переменные х 2 и х 4 к нулю: х 2 = х 4 = 0. Тогда из формулы х 1 = 4/5 – (1/5)*х 4 следует, что х 1 = 4/5, а из формулы х 2 = -17/5 + х 3 - - (7/5)*х 4 = -17/5 + х 3 следует, что х 3 = х 2 +17/5 = 17/5. Таким образом, мы получим базисное решение (4/5; 0; 17/5; 0).

Аналогично можно получить базисные решения для базисных переменных х 1 и х 4 – (9/7; 0; 0; -17/7); х 2 и х 4 – (0; -9; 0; 4); х 3 и х 4 – (0; 0; 9; 4).

Переменные х 2 и х 3 в этом примере нельзя взять в качестве базисных, так как ранг соответствующей матрицы равен единице, т.е. меньше двух:

Возможен и другой подход к определению того, можно или нет составить базис из некоторых переменных. При решении примера в итоге преобразования матрицы системы к ступенчатому виду она приняла вид:

Выбирая пары переменных, можно было рассчитать соответствующие миноры этой матрицы. Легко убедиться, что для всех пар, кроме х 2 и х 3 , они не равны нулю, т.е. столбцы линейно независимы. И только для столбцов при переменных х 2 и х 3
, что говорит об их линейной зависимости.

Рассмотрим еще один пример. Решим систему уравнений

Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво - оно привелось к неверному равенству 0 = -1, следовательно, данная система несовместна.

Метод Жордана-Гаусса 3 представляет собой развитие метода Гаусса. Суть его состоит в том, что расширенную матрицу системы преобразуют к виду, когда коэффициенты приrпеременных образуют единичную матрицу с точностью до перестановки строк или столбцов 4 (гдеr– ранг матрицы системы).

Решим этим методом систему:

Рассмотрим расширенную матрицу системы:

В этой матрице выберем единичный элемент. Например, коэффициент при х 2 в третьем ограничении 5 . Добьемся, чтобы в остальных строках в этом столбце стояли нули, т.е. сделаем столбец единичным. В процессе преобразований будем называть этотстолбец разрешающим (ведущим, ключевым). Третье ограничение (третьюстроку ) тоже будем называтьразрешающей . Самэлемент , который стоит на пересечении разрешающих строки и столбца (здесь это единица), тоже называютразрешающим .

В первой строке сейчас стоит коэффициент (-1). Чтобы получить на его месте ноль, умножим третью строку на (-1) и вычтем результат из первой строки (т.е. просто сложим первую строку с третьей).

Во второй строке стоит коэффициент 2. Чтобы получить на его месте ноль, умножим третью строку на 2 и вычтем результат из первой строки.

Результат преобразований будет иметь вид:

Из этой матрицы хорошо видно, что одно из первых двух ограничений можно вычеркнуть (соответствующие строки пропорциональны, т.е. эти уравнения следуют друг из друга). Вычеркнем, например, второе:

Итак, в новой системе два уравнения. Получен единичный столбец (второй), причем единица здесь стоит во второй строке. Запомним, что второму уравнению новой системы у нас будет соответствовать базисная переменная х 2 .

Выберем базисную переменную для первой строки. Это может быть любая переменная, кроме х 3 (потому что при х 3 в первом ограничении стоит нулевой коэффициент, т.е. набор переменных х 2 и х 3 здесь базисным быть не может). Можно взять первую или четвертую переменную.

Выберем х 1 . Тогда разрешающим элементом будет 5, и обе части разрешающего уравнения придется разделить на пять, чтобы получить в первом столбце первой строки единицу.

Добьемся, чтобы в остальных строках (т.е. во второй строке) в первом столбце стояли нули. Так как сейчас во второй строке стоит не ноль, а 3, надо вычесть из второй строки элементы преобразованной первой строки, умноженные на 3:

Из полученной матрицы можно непосредственно извлечь одно базисное решение, приравняв небазисные переменные к нулю, а базисные – к свободным членам в соответствующих уравнениях: (0,8; -3,4; 0; 0). Можно также вывести общие формулы, выражающие базисные переменные через небазисные: х 1 = 0,8 – 1,2х 4 ; х 2 = -3,4 + х 3 + 1,6х 4 . Эти формулы описывают все бесконечное множество решений системы (приравнивая х 3 и х 4 к произвольным числам, можно вычислить х 1 и х 2).

Отметим, что суть преобразований на каждом этапе метода Жордана-Гаусса заключалась в следующем:

1) разрешающую строку делили на разрешающий элемент, чтобы получить на его месте единицу,

2) из всех остальных строк вычитали преобразованную разрешающую, умноженную на тот элемент, который стоял в данной строке в разрешающем столбце, чтобы получить на месте этого элемента ноль.

Рассмотрим еще раз преобразованную расширенную матрицу системы:

Из этой записи видно, что ранг матрицы системы А равен r.

В ходе проведенных рассуждений мы установили, что система будет совместной тогда и только тогда, когда
. Это означает, что расширенная матрица системы будет иметь вид:

Отбрасывая нулевые строки, мы получим, что ранг расширенной матрицы системы тоже равен r.

Теорема Кронекера-Капелли . Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

Вспомним, что ранг матрицы равен максимальному числу ее линейно независимых строк. Из этого следует, что если ранг расширенной матрицы меньше числа уравнений, то уравнения системы линейно зависимы, и одно или несколько из них могут быть исключены из системы (поскольку являются линейной комбинацией остальных). Система уравнений будет линейно независимой лишь в том случае, если ранг расширенной матрицы равен числу уравнений.

При этом для совместных систем линейных уравнений можно утверждать, что если ранг матрицы равен числу переменных, то система имеет единственное решение, а если он меньше числа переменных, то система неопределенная и имеет бесконечно много решений.

1Например, пусть в матрице пять строк (исходный порядок строк – 12345). Надо поменять вторую строку и пятую. Чтобы вторая строка попала на место пятой, «сдвинулась» вниз, последовательно три раза поменяем соседние строки: вторую и третью (13245), вторую и четвертую (13425) и вторую и пятую (13452). Затем, чтобы пятая строка попала на место второй в исходной матрице, надо «сдвинуть» вверх пятую строку путем только двух последовательных перемен: пятой и четвертой строк (13542) и пятой и третьей (15342).

2Числом сочетаний из n по r называют число всех различных r–элементных подмножеств n–элементного множества (различными множествами считаются те, которые имеют различный состав элементов, порядок отбора при этом не важен). Его вычисляют по формуле:
. Напомним смысл знака “!” (факториал):
0!=1.)

3Поскольку этот метод более распространен, чем рассмотренный ранее метод Гаусса, и по своей сути представляет собой сочетание прямого и обратного хода метода Гаусса, его тоже иногда называют методом Гаусса, опуская первую часть названия.

4Например,
.

5Если бы в матрице системы не было единиц, то можно было бы, например, разделить обе части первого уравнения на два, и тогда первый коэффициент стал бы единичным; или т.п.

Решение систем линейных алгебраических уравнений (СЛАУ), несомненно, является важнейшей темой курса линейной алгебры. Огромное количество задач из всех разделов математики сводится к решению систем линейных уравнений. Этими факторами объясняется причина создания данной статьи. Материал статьи подобран и структурирован так, что с его помощью Вы сможете

подобрать оптимальный метод решения Вашей системы линейных алгебраических уравнений,
изучить теорию выбранного метода,
решить Вашу систему линейных уравнений, рассмотрев подробно разобранные решения характерных примеров и задач.

Краткое описание материала статьи.

Сначала дадим все необходимые определения, понятия и введем обозначения.

Далее рассмотрим методы решения систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных переменных и которые имеют единственное решение. Во-первых, остановимся на методе Крамера, во-вторых, покажем матричный метод решения таких систем уравнений, в-третьих, разберем метод Гаусса (метод последовательного исключения неизвестных переменных). Для закрепления теории обязательно решим несколько СЛАУ различными способами.

После этого перейдем к решению систем линейных алгебраических уравнений общего вида, в которых число уравнений не совпадает с числом неизвестных переменных или основная матрица системы является вырожденной. Сформулируем теорему Кронекера - Капелли, которая позволяет установить совместность СЛАУ. Разберем решение систем (в случае их совместности) с помощью понятия базисного минора матрицы. Также рассмотрим метод Гаусса и подробно опишем решения примеров.

Обязательно остановимся на структуре общего решения однородных и неоднородных систем линейных алгебраических уравнений. Дадим понятие фундаментальной системы решений и покажем, как записывается общее решение СЛАУ с помощью векторов фундаментальной системы решений. Для лучшего понимания разберем несколько примеров.

В заключении рассмотрим системы уравнений, сводящиеся к линейным, а также различные задачи, при решении которых возникают СЛАУ.

Навигация по странице.

Определения, понятия, обозначения.

Будем рассматривать системы из p линейных алгебраических уравнений с n неизвестными переменными (p может быть равно n ) вида

Неизвестные переменные, - коэффициенты (некоторые действительные или комплексные числа), - свободные члены (также действительные или комплексные числа).

Такую форму записи СЛАУ называют координатной .

В матричной форме записи эта система уравнений имеет вид ,
где - основная матрица системы, - матрица-столбец неизвестных переменных, - матрица-столбец свободных членов.

Если к матрице А добавить в качестве (n+1)-ого столбца матрицу-столбец свободных членов, то получим так называемую расширенную матрицу системы линейных уравнений. Обычно расширенную матрицу обозначают буквой Т , а столбец свободных членов отделяют вертикальной линией от остальных столбцов, то есть,

Решением системы линейных алгебраических уравнений называют набор значений неизвестных переменных , обращающий все уравнения системы в тождества. Матричное уравнение при данных значениях неизвестных переменных также обращается в тождество .

Если система уравнений имеет хотя бы одно решение, то она называется совместной .

Если система уравнений решений не имеет, то она называется несовместной .

Если СЛАУ имеет единственное решение, то ее называют определенной ; если решений больше одного, то – неопределенной .

Если свободные члены всех уравнений системы равны нулю , то система называется однородной , в противном случае – неоднородной .

Решение элементарных систем линейных алгебраических уравнений.

Если число уравнений системы равно числу неизвестных переменных и определитель ее основной матрицы не равен нулю, то такие СЛАУ будем называть элементарными . Такие системы уравнений имеют единственное решение, причем в случае однородной системы все неизвестные переменные равны нулю.

Такие СЛАУ мы начинали изучать в средней школе. При их решении мы брали какое-нибудь одно уравнение, выражали одну неизвестную переменную через другие и подставляли ее в оставшиеся уравнения, следом брали следующее уравнение, выражали следующую неизвестную переменную и подставляли в другие уравнения и так далее. Или пользовались методом сложения, то есть, складывали два или более уравнений, чтобы исключить некоторые неизвестные переменные. Не будем подробно останавливаться на этих методах, так как они по сути являются модификациями метода Гаусса.

Основными методами решения элементарных систем линейных уравнений являются метод Крамера, матричный метод и метод Гаусса. Разберем их.

Решение систем линейных уравнений методом Крамера.

Пусть нам требуется решить систему линейных алгебраических уравнений

в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть, .

Пусть - определитель основной матрицы системы, а - определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов:

При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как . Так находится решение системы линейных алгебраических уравнений методом Крамера.

Пример.

Методом Крамера .

Решение.

Основная матрица системы имеет вид . Вычислим ее определитель (при необходимости смотрите статью ):

Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.

Составим и вычислим необходимые определители (определитель получаем, заменив в матрице А первый столбец на столбец свободных членов , определитель - заменив второй столбец на столбец свободных членов, - заменив третий столбец матрицы А на столбец свободных членов):

Находим неизвестные переменные по формулам :

Ответ:

Основным недостатком метода Крамера (если это можно назвать недостатком) является трудоемкость вычисления определителей, когда число уравнений системы больше трех.

Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).

Пусть система линейных алгебраических уравнений задана в матричной форме , где матрица A имеет размерность n на n и ее определитель отличен от нуля.

Так как , то матрица А – обратима, то есть, существует обратная матрица . Если умножить обе части равенства на слева, то получим формулу для нахождения матрицы-столбца неизвестных переменных . Так мы получили решение системы линейных алгебраических уравнений матричным методом.

Пример.

Решите систему линейных уравнений матричным методом.

Решение.

Перепишем систему уравнений в матричной форме:

Так как

то СЛАУ можно решать матричным методом. С помощью обратной матрицы решение этой системы может быть найдено как .

Построим обратную матрицу с помощью матрицы из алгебраических дополнений элементов матрицы А (при необходимости смотрите статью ):

Осталось вычислить - матрицу неизвестных переменных, умножив обратную матрицу на матрицу-столбец свободных членов (при необходимости смотрите статью ):

Ответ:

или в другой записи x 1 = 4, x 2 = 0, x 3 = -1 .

Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего.

Решение систем линейных уравнений методом Гаусса.

Пусть нам требуется найти решение системы из n линейных уравнений с n неизвестными переменными
определитель основной матрицы которой отличен от нуля.

Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x 1 из всех уравнений системы, начиная со второго, далее исключается x 2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная x n . Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса . После завершения прямого хода метода Гаусса из последнего уравнения находится x n , с помощью этого значения из предпоследнего уравнения вычисляется x n-1 , и так далее, из первого уравнения находится x 1 . Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса .

Кратко опишем алгоритм исключения неизвестных переменных.

Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x 1 из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-ому уравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид

где , а .

К такому же результату мы бы пришли, если бы выразили x 1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x 1 исключена из всех уравнений, начиная со второго.

Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке

Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому уравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид

где , а . Таким образом, переменная x 2 исключена из всех уравнений, начиная с третьего.

Далее приступаем к исключению неизвестной x 3 , при этом действуем аналогично с отмеченной на рисунке частью системы

Так продолжаем прямой ход метода Гаусса пока система не примет вид

С этого момента начинаем обратный ход метода Гаусса: вычисляем x n из последнего уравнения как , с помощью полученного значения x n находим x n-1 из предпоследнего уравнения, и так далее, находим x 1 из первого уравнения.

Пример.

Решите систему линейных уравнений методом Гаусса.

Решение.

Исключим неизвестную переменную x 1 из второго и третьего уравнения системы. Для этого к обеим частям второго и третьего уравнений прибавим соответствующие части первого уравнения, умноженные на и на соответственно:

Теперь из третьего уравнения исключим x 2 , прибавив к его левой и правой частям левую и правую части второго уравнения, умноженные на :

На этом прямой ход метода Гаусса закончен, начинаем обратный ход.

Из последнего уравнения полученной системы уравнений находим x 3 :

Из второго уравнения получаем .

Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса .

Ответ:

X 1 = 4, x 2 = 0, x 3 = -1 .

Решение систем линейных алгебраических уравнений общего вида.

В общем случае число уравнений системы p не совпадает с числом неизвестных переменных n :

Такие СЛАУ могут не иметь решений, иметь единственное решение или иметь бесконечно много решений. Это утверждение относится также к системам уравнений, основная матрица которых квадратная и вырожденная.

Теорема Кронекера – Капелли.

Прежде чем находить решение системы линейных уравнений необходимо установить ее совместность. Ответ на вопрос когда СЛАУ совместна, а когда несовместна, дает теорема Кронекера – Капелли :
для того, чтобы система из p уравнений с n неизвестными (p может быть равно n ) была совместна необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу расширенной матрицы, то есть, Rank(A)=Rank(T) .

Рассмотрим на примере применение теоремы Кронекера – Капелли для определения совместности системы линейных уравнений.

Пример.

Выясните, имеет ли система линейных уравнений решения.

Решение.

. Воспользуемся методом окаймляющих миноров. Минор второго порядка отличен от нуля. Переберем окаймляющие его миноры третьего порядка:

Так как все окаймляющие миноры третьего порядка равны нулю, то ранг основной матрицы равен двум.

В свою очередь ранг расширенной матрицы равен трем, так как минор третьего порядка

отличен от нуля.

Таким образом, Rang(A) , следовательно, по теореме Кронекера – Капелли можно сделать вывод, что исходная система линейных уравнений несовместна.

Ответ:

Система решений не имеет.

Итак, мы научились устанавливать несовместность системы с помощью теоремы Кронекера – Капелли.

А как же находить решение СЛАУ, если установлена ее совместность?

Для этого нам потребуется понятие базисного минора матрицы и теорема о ранге матрицы.

Минор наивысшего порядка матрицы А , отличный от нуля, называется базисным .

Из определения базисного минора следует, что его порядок равен рангу матрицы. Для ненулевой матрицы А базисных миноров может быть несколько, один базисный минор есть всегда.

Для примера рассмотрим матрицу .

Все миноры третьего порядка этой матрицы равны нулю, так как элементы третьей строки этой матрицы представляют собой сумму соответствующих элементов первой и второй строк.

Базисными являются следующие миноры второго порядка, так как они отличны от нуля

Миноры базисными не являются, так как равны нулю.

Теорема о ранге матрицы.

Если ранг матрицы порядка p на n равен r , то все элементы строк (и столбцов) матрицы, не образующие выбранный базисный минор, линейно выражаются через соответствующие элементы строк (и столбцов), образующих базисный минор.

Что нам дает теорема о ранге матрицы?

Если по теореме Кронекера – Капелли мы установили совместность системы, то выбираем любой базисный минор основной матрицы системы (его порядок равен r ), и исключаем из системы все уравнения, которые не образуют выбранный базисный минор. Полученная таким образом СЛАУ будет эквивалентна исходной, так как отброшенные уравнения все равно излишни (они согласно теореме о ранге матрицы являются линейной комбинацией оставшихся уравнений).

В итоге, после отбрасывания излишних уравнений системы, возможны два случая.

Если число уравнений r в полученной системе будет равно числу неизвестных переменных, то она будет определенной и единственное решение можно будет найти методом Крамера, матричным методом или методом Гаусса.

Пример.

Решение.

Ранг основной матрицы системы равен двум, так как минор второго порядка отличен от нуля. Ранг расширенной матрицы также равен двум, так как единственный минор третьего порядка равен нулю

а рассмотренный выше минор второго порядка отличен от нуля. На основании теоремы Кронекера – Капелли можно утверждать совместность исходной системы линейных уравнений, так как Rank(A)=Rank(T)=2 .

В качестве базисного минора возьмем . Его образуют коэффициенты первого и второго уравнений:

Третье уравнение системы не участвует в образовании базисного минора, поэтому исключим его из системы на основании теоремы о ранге матрицы:

Так мы получили элементарную систему линейных алгебраических уравнений. Решим ее методом Крамера:

Ответ:

x 1 = 1, x 2 = 2 .

Если число уравнений r в полученной СЛАУ меньше числа неизвестных переменных n , то в левых частях уравнений оставляем слагаемые, образующие базисный минор, остальные слагаемые переносим в правые части уравнений системы с противоположным знаком.

Неизвестные переменные (их r штук), оставшиеся в левых частях уравнений, называются основными .

Неизвестные переменные (их n - r штук), которые оказались в правых частях, называются свободными .

Теперь считаем, что свободные неизвестные переменные могут принимать произвольные значения, при этом r основных неизвестных переменных будут выражаться через свободные неизвестные переменные единственным образом. Их выражение можно найти решая полученную СЛАУ методом Крамера, матричным методом или методом Гаусса.

Разберем на примере.

Пример.

Решите систему линейных алгебраических уравнений .

Решение.

Найдем ранг основной матрицы системы методом окаймляющих миноров. В качестве ненулевого минора первого порядка возьмем a 1 1 = 1 . Начнем поиск ненулевого минора второго порядка, окаймляющего данный минор:

Так мы нашли ненулевой минор второго порядка. Начнем поиск ненулевого окаймляющего минора третьего порядка:

Таким образом, ранг основной матрицы равен трем. Ранг расширенной матрицы также равен трем, то есть, система совместна.

Найденный ненулевой минор третьего порядка возьмем в качестве базисного.

Для наглядности покажем элементы, образующие базисный минор:

Оставляем в левой части уравнений системы слагаемые, участвующие в базисном миноре, остальные переносим с противоположными знаками в правые части:

Придадим свободным неизвестным переменным x 2 и x 5 произвольные значения, то есть, примем , где - произвольные числа. При этом СЛАУ примет вид

Полученную элементарную систему линейных алгебраических уравнений решим методом Крамера:

Следовательно, .

В ответе не забываем указать свободные неизвестные переменные.

Ответ:

Где - произвольные числа.

Подведем итог.

Чтобы решить систему линейных алгебраических уравнений общего вида, сначала выясняем ее совместность, используя теорему Кронекера – Капелли. Если ранг основной матрицы не равен рангу расширенной матрицы, то делаем вывод о несовместности системы.

Если ранг основной матрицы равен рангу расширенной матрицы, то выбираем базисный минор и отбрасываем уравнения системы, которые не участвуют в образовании выбранного базисного минора.

Если порядок базисного минора равен числу неизвестных переменных, то СЛАУ имеет единственное решение, которое находим любым известным нам методом.

Если порядок базисного минора меньше числа неизвестных переменных, то в левой части уравнений системы оставляем слагаемые с основными неизвестными переменными, остальные слагаемые переносим в правые части и придаем свободным неизвестным переменным произвольные значения. Из полученной системы линейных уравнений находим основные неизвестные переменные методом Крамера, матричным методом или методом Гаусса.

Метод Гаусса для решения систем линейных алгебраических уравнений общего вида.

Методом Гаусса можно решать системы линейных алгебраических уравнений любого вида без предварительного их исследования на совместность. Процесс последовательного исключения неизвестных переменных позволяет сделать вывод как о совместности, так и о несовместности СЛАУ, а в случае существования решения дает возможность отыскать его.

С точки зрения вычислительной работы метод Гаусса является предпочтительным.

Смотрите его подробное описание и разобранные примеры в статье метод Гаусса для решения систем линейных алгебраических уравнений общего вида .

Запись общего решения однородных и неоднородных систем линейных алгебраических с помощью векторов фундаментальной системы решений.

В этом разделе речь пойдет о совместных однородных и неоднородных системах линейных алгебраических уравнений, имеющих бесконечное множество решений.

Разберемся сначала с однородными системами.

Фундаментальной системой решений однородной системы из p линейных алгебраических уравнений с n неизвестными переменными называют совокупность (n – r) линейно независимых решений этой системы, где r – порядок базисного минора основной матрицы системы.

Если обозначить линейно независимые решения однородной СЛАУ как X (1) , X (2) , …, X (n-r) (X (1) , X (2) , …, X (n-r) – это матрицы столбцы размерности n на 1 ), то общее решение этой однородной системы представляется в виде линейной комбинации векторов фундаментальной системы решений с произвольными постоянными коэффициентами С 1 , С 2 , …, С (n-r) , то есть, .

Что обозначает термин общее решение однородной системы линейных алгебраических уравнений (орослау)?

Смысл прост: формула задает все возможные решения исходной СЛАУ, другими словами, взяв любой набор значений произвольных постоянных С 1 , С 2 , …, С (n-r) , по формуле мы получим одно из решений исходной однородной СЛАУ.

Таким образом, если мы найдем фундаментальную систему решений, то мы сможем задать все решения этой однородной СЛАУ как .

Покажем процесс построения фундаментальной системы решений однородной СЛАУ.

Выбираем базисный минор исходной системы линейных уравнений, исключаем все остальные уравнения из системы и переносим в правые части уравнений системы с противоположными знаками все слагаемые, содержащие свободные неизвестные переменные. Придадим свободным неизвестным переменным значения 1,0,0,…,0 и вычислим основные неизвестные, решив полученную элементарную систему линейных уравнений любым способом, например, методом Крамера. Так будет получено X (1) - первое решение фундаментальной системы. Если придать свободным неизвестным значения 0,1,0,0,…,0 и вычислить при этом основные неизвестные, то получим X (2) . И так далее. Если свободным неизвестным переменным придадим значения 0,0,…,0,1 и вычислим основные неизвестные, то получим X (n-r) . Так будет построена фундаментальная система решений однородной СЛАУ и может быть записано ее общее решение в виде .

Для неоднородных систем линейных алгебраических уравнений общее решение представляется в виде , где - общее решение соответствующей однородной системы, а - частное решение исходной неоднородной СЛАУ, которое мы получаем, придав свободным неизвестным значения 0,0,…,0 и вычислив значения основных неизвестных.

Разберем на примерах.

Пример.

Найдите фундаментальную систему решений и общее решение однородной системы линейных алгебраических уравнений .

Решение.

Ранг основной матрицы однородных систем линейных уравнений всегда равен рангу расширенной матрицы. Найдем ранг основной матрицы методом окаймляющих миноров. В качестве ненулевого минора первого порядка возьмем элемент a 1 1 = 9 основной матрицы системы. Найдем окаймляющий ненулевой минор второго порядка:

Минор второго порядка, отличный от нуля, найден. Переберем окаймляющие его миноры третьего порядка в поисках ненулевого:

Все окаймляющие миноры третьего порядка равны нулю, следовательно, ранг основной и расширенной матрицы равен двум. Базисным минором возьмем . Отметим для наглядности элементы системы, которые его образуют:

Третье уравнение исходной СЛАУ не участвует в образовании базисного минора, поэтому, может быть исключено:

Оставляем в правых частях уравнений слагаемые, содержащие основные неизвестные, а в правые части переносим слагаемые со свободными неизвестными:

Построим фундаментальную систему решений исходной однородной системы линейных уравнений. Фундаментальная система решений данной СЛАУ состоит из двух решений, так как исходная СЛАУ содержит четыре неизвестных переменных, а порядок ее базисного минора равен двум. Для нахождения X (1) придадим свободным неизвестным переменным значения x 2 = 1, x 4 = 0 , тогда основные неизвестные найдем из системы уравнений
.

Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.

Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.

Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.

Линейное уравнение

Уравнения вида ax+by=c называют линейными. Обозначения x, y - это неизвестные, значение которых надо найти, b, a - коэффициенты при переменных, c - свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.

Виды систем линейных уравнений

Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.

F1(x, y) = 0 и F2(x, y) = 0, где F1,2 - функции, а (x, y) - переменные функций.

Решить систему уравнений - это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.

Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.

Если системы имеют одно общее решение или решения не существует их называют равносильными.

Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака "равенство" часть имеет значение или выражена функцией, такая система неоднородна.

Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.

Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.

Простые и сложные методы решения систем уравнений

Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.

Основная задача при обучении способам решения - это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода

Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.

Решение систем методом подстановки

Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе

Приведем решение примера системы линейных уравнений 7 класса методом подстановки:

Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.

Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.

Решение примера системы линейных неоднородных уравнений:

Решение с помощью алгебраического сложения

При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.

Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.

Алгоритм действий решения:

Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.
Почленно сложить полученное выражение и найти одно из неизвестных.
Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.

Способ решения введением новой переменной

Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.

Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.

Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.

Необходимо найти значение дискриминанта по известной формуле: D = b2 - 4*a*c, где D - искомый дискриминант, b, a, c - множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.

Решение для полученных в итоге системы находят методом сложения.

Наглядный метод решения систем

Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.

Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.

Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.

Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.

В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.

Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.

Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.

Матрица и ее разновидности

Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. n*m имеет n - строк и m - столбцов.

Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей - вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.

Обратная матрица - это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.

Правила преобразования системы уравнений в матрицу

Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение - одна строка матрицы.

Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.

Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y - только во второй.

При умножении матрицы все элементы матрицы последовательно умножаются на число.

Варианты нахождения обратной матрицы

Формула нахождения обратной матрицы довольно проста: K -1 = 1 / |K|, где K -1 - обратная матрица, а |K| - определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.

Определитель легко вычисляется для матрицы "два на два", необходимо лишь помножить друг на друга элементы по диагонали. Для варианта "три на три" существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.

Решение примеров систем линейных уравнений матричным методом

Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.

В примере a nm - коэффициенты уравнений, матрица - вектор x n - переменные, а b n - свободные члены.

Решение систем методом Гаусса

В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса - Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.

Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 - соответственно с 3-мя и 4-мя переменными.

После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.

В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:

Как видно из примера, на шаге (3) было получено два уравнения 3x 3 -2x 4 =11 и 3x 3 +2x 4 =7. Решение любого из уравнений позволит узнать одну из переменных x n .

Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.

Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.

Для простоты записи вычислений принято делать следующим образом:

Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.

Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака "стрелка" и продолжают выполнять необходимые алгебраические действия до достижения результата.

В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.

Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.

Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.

Материал этой статьи предназначен для первого знакомства с системами уравнений. Здесь мы введем определение системы уравнений и ее решений, а также рассмотрим наиболее часто встречающиеся виды систем уравнений. По обыкновению будем приводить поясняющие примеры.

Навигация по странице.

Что такое система уравнений?

К определению системы уравнений будем подбираться постепенно. Сначала лишь скажем, что его удобно дать, указав два момента: во-первых, вид записи, и, во-вторых, вложенный в эту запись смысл. Остановимся на них по очереди, а затем обобщим рассуждения в определение систем уравнений.

Пусть перед нами несколько каких-нибудь . Для примера возьмем два уравнения 2·x+y=−3 и x=5 . Запишем их одно под другим и объединим слева фигурной скобкой:

Записи подобного вида, представляющие собой несколько расположенных в столбик уравнений и объединенных слева фигурной скобкой, являются записями систем уравнений.

Что же означают такие записи? Они задают множество всех таких решений уравнений системы, которые являются решением каждого уравнения.

Не помешает описать это другими словами. Допустим, какие-то решения первого уравнения являются решениями и всех остальных уравнений системы. Так вот запись системы как раз их и обозначает.

Теперь мы готовы достойно воспринять определение системы уравнений.

Определение.

Системами уравнений называют записи, представляющие собой расположенные друг под другом уравнения, объединенные слева фигурной скобкой, которые обозначают множество всех решений уравнений, одновременно являющихся решениями каждого уравнения системы.

Аналогичное определение приведено в учебнике , однако там оно дано не для общего случая, а для двух рациональных уравнений с двумя переменными.

Основные виды

Понятно, что разнообразных уравнений бесконечно много. Естественно, и составленных с их использованием систем уравнений также бесконечно много. Поэтому, для удобства изучения и работы с системами уравнений есть смысл их разделить на группы по схожим характеристикам, а дальше перейти к рассмотрению систем уравнений отдельных видов.

Первое подразделение напрашивается по числу уравнений, входящих в систему. Если уравнений два, то можно сказать, что перед нами система двух уравнений, если три – то система трех уравнений, и т.д. Понятно, что не имеет смысла говорить о системе одного уравнения, так как в этом случае по сути мы имеем дело с самим уравнением, а не с системой.

Следующее деление базируется на числе переменных, участвующих в записи уравнений системы. Если переменная одна, то мы имеем дело с системой уравнений с одной переменной (еще говорят с одной неизвестной), если две – то с системой уравнений с двумя переменными (с двумя неизвестными), и т.д. Например, - это система уравнений с двумя переменными x и y .

При этом имеется в виду число всех различных переменных, участвующих в записи. Они не обязательно должны все сразу входить в запись каждого уравнения, достаточно их наличия хотя бы в одном уравнении. К примеру, - это система уравнений с тремя переменными x , y и z . В первом уравнение переменная x присутствует явно, а y и z – неявно (можно считать, что эти переменные имеют нуль), а во втором уравнении есть x и z , а переменная y явно не представлена. Другими словами, первое уравнение можно рассматривать как , а второе – как x+0·y−3·z=0 .

Третий момент, в котором различаются системы уравнений, это вид самих уравнений.

В школе изучение систем уравнений начинается с систем двух линейных уравнений с двумя переменными . То есть, такие системы составляют два линейных уравнения. Вот пара примеров: и . На них и познаются азы работы с системами уравнений.

При решении более сложных задач можно столкнуться и с системами трех линейных уравнений с тремя неизвестными.

Дальше в 9 классе в системы двух уравнений с двумя переменными добавляются нелинейные уравнения, по большей части целые уравнения второй степени, реже – более высоких степеней. Эти системы называют системами нелинейных уравнений, при необходимости уточняют число уравнений и неизвестных. Покажем примеры таких систем нелинейных уравнений: и .

А дальше в системах встречаются и , к примеру, . Их обычно называют просто системами уравнений, не уточняя, каких именно уравнений. Здесь стоит заметить, что наиболее часто про систему уравнений говорят просто «система уравнений», а уточнения добавляют лишь при необходимости.

В старших классах по мере изучения материала в системы проникают иррациональные, тригонометрические, логарифмические и показательные уравнения : , , .

Если заглянуть еще дальше в программу первых курсов ВУЗов, то основной упор сделан на исследование и решение систем линейных алгебраических уравнений (СЛАУ) , то есть, уравнений, в левых частях которых многочлены первой степени, а в правых – некоторые числа. Но там, в отличие от школы, уже берутся не два линейных уравнения с двумя переменными, а произвольное число уравнений с произвольным числом переменных, зачастую не совпадающим с числом уравнений .

Что называется решением системы уравнений?

К системам уравнений непосредственно относится термин «решение системы уравнений». В школе дается определение решения системы уравнений с двумя переменными :

Определение.

Решением системы уравнений с двумя переменными называется пара значений этих переменных, обращающая каждое уравнение системы в верное , другими словами, являющаяся решением каждого уравнения системы.

Например, пара значений переменных x=5 , y=2 (ее можно записать как (5, 2) ) является решением системы уравнений по определению, так как уравнения системы при подстановке в них x=5 , y=2 обращаются в верные числовые равенства 5+2=7 и 5−2=3 соответственно. А вот пара значений x=3 , y=0 не является решением этой системы, так как при подстановке этих значений в уравнения, первое из них обратится в неверное равенство 3+0=7 .

Аналогичные определения можно сформулировать и для систем с одной переменной, а также для систем с тремя, четырьмя и т.д. переменными.

Определение.

Решением системы уравнений с одной переменной будет значение переменной, являющееся корнем всех уравнений системы, то есть, обращающее все уравнения в верные числовые равенства.

Приведем пример. Рассмотрим систему уравнений с одной переменной t вида . Число −2 является ее решением, так как и (−2) 2 =4 , и 5·(−2+2)=0 – верные числовые равенства. А t=1 – не является решением системы, так как подстановка этого значения даст два неверных равенства 1 2 =4 и 5·(1+2)=0 .

Определение.

Решением системы с тремя, четырьмя и т.д. переменными называется тройка, четверка и т.д. значений переменных соответственно, обращающая в верные равенства все уравнения системы.

Так по определению тройка значений переменных x=1 , y=2 , z=0 – решение системы , так как 2·1=2 , 5·2=10 и 1+2+0=3 - верные числовые равенства. А (1, 0, 5) не является решением этой системы, так как при подстановке этих значений переменных в уравнения системы второе из них обращается в неверное равенство 5·0=10 , да и третье тоже 1+0+5=3 .

Заметим, что системы уравнений могут не иметь решений, могут иметь конечное число решений, например, одно, два, …, а могут иметь бесконечно много решений. В этом Вы убедитесь по мере углубления в тему.

Учитывая определения системы уравнений и их решений можно заключить, что решение системы уравнений представляет собой пересечение множеств решений всех ее уравнений.

В заключение приведем несколько связанных определений:

Определение.

несовместной , если она не имеет решений, в противном случае система называется совместной .

Определение.

Система уравнений называется неопределенной , если она имеет бесконечно много решений, и определенной , если имеет конечное число решений, либо не имеет их вообще.

Эти термины вводятся, например, в учебнике , однако в школе применяются довольно редко, чаще их можно услышать в высших учебных заведениях.

Список литературы.

Алгебра: учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 17-е изд. - М. : Просвещение, 2008. - 240 с. : ил. - ISBN 978-5-09-019315-3.
Алгебра: 9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 16-е изд. - М. : Просвещение, 2009. - 271 с. : ил. - ISBN 978-5-09-021134-5.
Мордкович А. Г. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. - 17-е изд., доп. - М.: Мнемозина, 2013. - 175 с.: ил. ISBN 978-5-346-02432-3.
Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. - 13-е изд., стер. - М.: Мнемозина, 2011. - 222 с.: ил. ISBN 978-5-346-01752-3.
Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. - 2-е изд., стер. - М.: Мнемозина, 2008. - 287 с.: ил. ISBN 978-5-346-01027-2.
Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
А. Г. Курош . Курс высшей алгебры.
Ильин В. А., Позняк Э. Г. Аналитическая геометрия: Учеб.: Для вузов. – 5-е изд. – М.: Наука. Физматлит, 1999. – 224 с. – (Курс высшей математики и мат. физики). – ISBN 5-02-015234 – X (Вып. 3)